ゲームに簡単なプログラムを組み込むためにスクリプト言語とそれを実行するインタープリタをC++で作ってしまおうというコーナーです。
解析木を作ればそれを元に実行できることがわかりましたが、その解析木を作るには構文解析が必須。
その構文解析をするための文法をプログラムでも書ける形で記述するには?
まとめてゆくこと
例えば、「15+7-2-2-(2+3)*12/(14-4)」を解釈するならば、これを、「15」「+」「7」「-」「2」「-」「2」「-」「(」「2」「+」「3」「)」「*」「12」「/」「(」「14」「-」「4」「)」に分解して、更にこれをちゃんと計算できるように構造を調べなければならないのです。
……なんというか、筋道立てて説明するのがなんとなく難しそうなので、「15+7-2-2-(2+3)*12/(14-4)」を使った実例でいっちゃいましょう。
まず「1」まで読みます。これは1という数字かもしれませんが後に何か数字が来ると別の数字になるかもしれません。
次に「5」が来ます。1じゃありませんでした。これは15かもしれません。
更に「+」が来ます。これは足し算になるかもしれません。先ほどの15はこれで15という数字に決定しました。
「7」が来ます。7という数字かもしれません。次に「-」が来るので7という数字で決定です。
「数字+数字」は足し算の形式になので足し算かもしれません。次に来るのが「-」なので後ろを先に計算するということはなさそうです。これは足し算と考えてよさそうです。「数字+数字」を「足し算の結果」としてまとめておきます。
これで、今のところ読み終わっているのは「足し算の結果-」です。
次に「2」がきて「-」が来ると2という数字が決定して、「足し算の結果-数字-」になり、「足し算の結果-数字」は「引き算の結果」でまとめられそうです。
こうやってまとめていくと、最終的に「引き算の結果」となります。
こうやってまとめますまとめますと文章ばかり見ているとどんなことになっているかわかりにくいので図にして見ましょう。
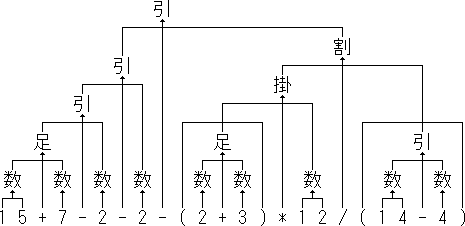
図にしてみるとなんとなく前回の解析木に似ているような気がします。似ていなくても少なくとも前回の解析木のように書き換えるのは容易そうです。
括弧は計算の順序を変えるだけなので何も計算はしていません。
BNF記法
このまとめていくためのルールを生成規則といったりします。いえ、本当は逆で、生成規則で式を作ることができればその逆の作業でまとめていくことができるのです。
そしてこの規則は、BNF記法や、拡張BNF記法で書かれることが多いそうです。
まあ、記述方法は言葉で説明してもあまり難しいものではないのですが、めんどいのでググってください。といいたかったのですが、軽く探してみたところ「BNFとはバッカス・ナウア記法のことである」的な説明ばかりがヒットしたのでしぶしぶ自分で説明します(ちなみに、「BNF記法入門(1) ─XML関連仕様を読むために─」がざっと調べた中では最もしっかり説明がなされていました。BNFを使いやすく拡張したEBNFには数々の方言がありますが今回はとりあえずこれに書いている記法に準じます)。
- A ::= B
- AはBである。
- 'abc'
- 「abc」という文字列。
- A B
- Aの直後にBが続いたもの。
- A | B
- AまたはB。
- A B | C D
- Aの直後にBが続いたものまたはCの直後にDが続いたもの。
- A (B | C)
- Aの直後にBまたはCが続いたもの。
- A?
- Aが0個または1個(EBNF)。
- A*
- Aが0個以上(EBNF)。
- A+
- Aが1個以上(EBNF)。
今回の数式のBNFを少し考えてみましょう(便宜上番号を振っています)。
まず、数はこうなるでしょう。
(1) 数字 ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(2) 非ゼロ数字 ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(3) 数 ::= 非ゼロ数字 数字*正の整数しか対応できてないけどここではほっときます。
数式の表現ですが、まずは足し算と引き算に対応してみます。
+と-は意味は反対ですが似たもの同士なので一緒くたに扱います。
(1) 数字 ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(2) 非ゼロ数字 ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(3) 数 ::= 非ゼロ数字 数字*
(4) 式 ::= 数 ('+' | '-') 数単純に考えて、数と数を足したり引いたりしてみました。
しかしこれでは最初の「15+7」までしかまとめられません。
この後ろには「-2」とか、まだまだ足したり引いたりしなきゃいけないものがいっぱいあります。
とりあえず「式」の後ろにもっとくっつけてみましょう。
(1) 数字 ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(2) 非ゼロ数字 ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(3) 数 ::= 非ゼロ数字 数字*
(4) 式 ::= 数 | 式 ('+' | '-') 数えーっと、ややこしいですが、右辺のほうの「式」に「式 ::= 数 | 式 ('+' | '-') 数」を代入すると、「式 ::= 数 | (数 | 式 ('+' | '-') 数) ('+' | '-') 数」となり、「数 '+' 数 '-' 数」の形式の「15+7-2」にも対応できるようになりました。
「式」に「式」を代入し続ければいくらでも長い式が作れます。
ただ、今のままでは「数」の代わりに掛け算割り算がやってきたらなすすべがありません。
「数」の部分を置き換えて掛け算と割り算にも対応しましょう。
(1) 数字 ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(2) 非ゼロ数字 ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(3) 数 ::= 非ゼロ数字 数字*
(4) 式 ::= 項 | 式 ('+' | '-') 項
(5) 項 ::= 数 | 項 ('*' | '/') 数ほぼ同じ要領ですね。これでも単なる足し算は表せます。
しかし、まだ括弧入りの足し算引き算とかには対応してません。
括弧の中には、足し算引き算掛け算割り算なんでも入ってしまいます。
それも考慮して書いてみましょう。
(1) 数字 ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(2) 非ゼロ数字 ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
(3) 数 ::= 非ゼロ数字 数字*
(4) 式 ::= 項 | 式 ('+' | '-') 項
(5) 項 ::= 因子 | 項 ('*' | '/') 因子
(6) 因子 ::= 数 | '(' 式 ')'わかりにくいですね。BNFの括弧なのか、数式の中の括弧か、一目じゃわかりません。
ま、そこはそれ、じっくり見ればいいだけの話で、文法自体に問題があるわけじゃないと思うので些細な問題として無視しましょう。
とりあえず、今回の例で使った「15+7-2-2-(2+3)*12/(14-4)」の数式はこれで表せるようになったはずです。
ためしに例としてあげたあの数式をこの規則を使ってまとめていきます。
・・・・と思ったのですが、手間が半端じゃなかったので断念。途中まで頑張った記録を見たければソースをご覧くださいまし(所々間違ってるかも)。
実際のスクリプトではもっと複雑な規則を使います。