はじめに
最終的にやりたいこと
三次元空間における二線分間の距離を求めることが今回の目標です。
なお、この問題は、いくつかの場合によって異なる計算を行う必要があるので、二線分間の距離を求める唯一つの式というのは(式自体が場合分けを含んでいない限り)存在しません。
そのため、このページでは線分同士の位置関係で場合分けをしてそれぞれについて距離を求めています。
前提となる知識
- 三次元ベクトルの基本的な知識
- このページにおける計算では、x、y、z といった個別の座標は計算に用いません。
計算は基本的に全てベクトルについて行うので、ベクトルに関する最低限の知識は必要になります。 - 二点間の距離
- はっきり言って三次元ベクトルの基本的な知識のひとつなのですが、改めてはっきりとさせておきます。
一応、二つの位置ベクトルの差の大きさで計算できます。 - 線分と点の距離
- これも分かっていることが前提…と言いたい所ですが、二線分間の距離の特別な場合として、一方の線分が点に縮退している場合があるので、その際に改めて計算します。
記号と用語の定義
ベクトルに関する記号や用語には様々な記述法があり、統一されていません。
そのため、混乱を避けるため、ここで使用する記号や用語について、ここに記述しておきます。
| 1 | 定数 1 を表します。 装飾のない数字は定数を表すものとします。 |
| a | 実数変数 a を表します。 斜小文字一文字の場合は実数変数を表すものとします。 |
| a1 | 実数変数 a1 を表します。 下付き文字は添字として関連のある複数の変数の区別に使います。 ベクトルについても同じとします。 |
| a2 | 実数変数 a の 2 乗を表します。 上付き数字は累乗を表すものとします。 |
| a・b ab | 実数変数 a と実数変数 b の積を表します。 実数同士の積には省略可能な「・」を使用することにします。 |
| |a| | 実数 a の絶対値を表します。 絶対値を表す記号としては「|」を使用するものとします。 |
| A | 点 A の位置ベクトルを表します。 太大文字一文字の場合は位置ベクトルを表すものとします。 |
| AB | 点 A から点 B へ向かうベクトル(AB = B - A)を表します。 太大文字二文字の場合は二点で定義されるベクトルを表すものとします。 |
| a | 位置ベクトルでない通常のベクトル a を表します。 太小文字一文字の場合は位置ベクトルを表すものとします。 |
| |a| | ベクトル a の大きさを表します。 ベクトルの大きさを表す記号としては「|」を使用するものとします。 |
| det(a b c) | ベクトル a、b、c を行列の列ベクトルとして用いた場合の三行三列の行列に対する行列式を表します。 行列式を表す場合関数の形式で表します。 |
| a・b | ベクトル a とベクトル b の内積を表します。 内積を表す記号としては「・」を使用し、省略しないものとします。 |
| a×b | ベクトル a とベクトル b の外積を表します。 外積を表す記号としては「×」を使用し、省略しないものとします。 |
| a・b ab | 実数変数 a とベクトル b の積を表します。 実数とベクトルの積には省略可能な「・」を使用することにします。 |
| func(x) | 実数変数 x を用いた関数 func を表します。 装飾のない一文字以上のアルファベットは関数を表すものとします。 |
| 絶対値 | 実数の絶対値またはベクトルの大きさを表すものとします。 |
| 縮退 | なにやら小難しい定義があるようではありますが、ここでは深く考えず本来別のものなのに同じようになっちゃったという状態を言うことにします。 以下のリンク先がなんとなく分かりやすいと思います。 縮退をわかりやすくお願いします -OKWave もっとも、今回は線分の両端が一致して一点になり、線分と呼べなくなった場合を言っているだけですが。 |
ここで用いる名称等
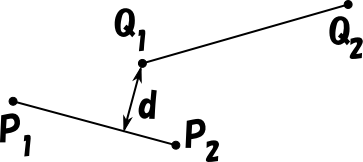
| P1、P2 | 線分 1 の端点です。 |
| Q1、Q2 | 線分 2 の端点です。 |
| t | 線分 1 に関する媒介変数で、以下の範囲をとります。 0 ≦ t ≦ 1 |
| u | 線分 2 に関する媒介変数で、以下の範囲をとります。 0 ≦ u ≦ 1 |
| P | 線分 1 上の任意の点で、位置は以下の式で表されます。 P = P1 + tP1P2 |
| Q | 線分 2 上の任意の点で、位置は以下の式で表されます。 Q = Q1 + uQ1Q2 |
| Pn | 線分 1 上の、線分 2 に最も近い点です。 |
| Qn | 線分 2 上の、線分 1 に最も近い点です。 |
| d | 線分 1 と線分 2 の距離です。 d = |PnQn| |
| R | なんでもいいからとにかく点です。 |
二次元の場合
なぜ二次元を考えるのか
最終的にやりたいことで述べたように、目的は三次元における線分同士の距離を得ることです。
なのになぜ今二次元について考えるのか、説明が必要でしょう。
ひとつに三次元へステップアップするための前段階という目的もありますが、本当の理由は、二線分が同一平面状に存在する特別な場合を考えるためです。
すなわち、二次元における二線分間の距離の計算は、三次元における計算の特別な場合なのです。
同一平面上にあるかどうかの判定
三次元空間中の二線分が同一平面上にあるかどうかを判定するには、二つの線分を構成する四点の位置関係を調べます。
でも自分で考えるのは面倒なのでネットで調べてみたら、こんなの見つけました。
R^2において、r1,r2を並べて作った2×2の正方行列の行列式は,r1,r2の張る平行四辺形の面積を表します。
同様に、R^3において、r1,r2,r3を並べて作った行列の行列式は、r1,r2,r3の張る平行六面体の体積を表します。
(4点が同一平面上にあることを示す問題 - 教えて!goo eatern27さんの回答より)
r1、r2、r3 はベクトルですので、ここでは r1 を P1P2、r2 を P1Q1、r3 を P1Q2 とおきましょう。
そうすると、四点 P1、P2、Q1、Q2 が同一平面上にある条件、すなわち線分 1、2 が同一平面上にある条件は、次のようになります。
det(P1P2 P1Q1 P1Q2) = 0
なお、この式は、線分が点に縮退している場合、つまり、P1 = P2 や Q1 = Q2 の場合にも成り立ちます。
一つの線分と一つの点の組は必ず同一平面上にあるということですね。
二線分が両方とも点に縮退している場合
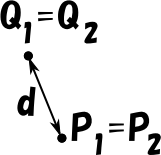
P1 = P2、Q1 = Q2 の場合です。
要するに、二点間の距離です。
P1 = P2、Q1 = Q2 の場合
d = |P1Q1|
一方の線分が点に縮退している場合
つまり、点と線分の距離です。
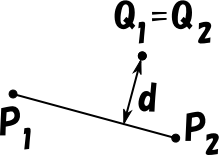
今回は、Q1 = Q2 の場合だけを考えます。
この場合、点 Q1 の位置により3つに場合分けできます。
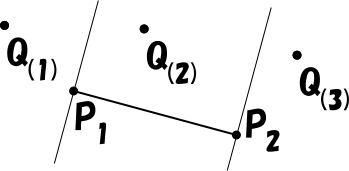
- Pn = P1 の場合
- Pn = P ( P = P1 + tP1P2、0 < t < 1 ) の場合
- Pn = P2 の場合
この3つの場合分けは、点 Q1 から直線 1 に下ろした垂線と直線 1 が交差する点 P の位置により決まります。
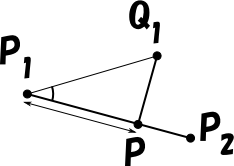
このとき、点 P1 から点 P までの距離 |P1P| は次のように表されます。
|P1P| = |P1Q1||cos∠Q1P1P2|
= |P1Q1・P1P2|/|P1P2|
(P1Q1・P1P2 = |P1Q1||P1P2|cos∠Q1P1P2 により)
距離ということで絶対値を求めましたが、cos∠Q1P1P2 の符号により (1) の位置にあるか (2) の位置にあるかが分かるので、以下のように d2 を定めます。
d2 = P1Q1・P1P2/|P1P2|
そうすると、先ほどの場合分けは次のように書き換えられます。
- d2 ≦ 0 の場合
- 0 < d2 < |P1P2| の場合
- d2 ≧ |P1P2| の場合
境界ではどちらでも同じ計算結果になるため、計算が簡単な方に含めています。
さて、このままでも別に良いのですが、d2 なんて新たな記号を用意したり絶対値計算があったり割り算が鬱陶しかったりするので、|P1P2| を各辺に掛けて式を単純化してみます。
- P1Q1・P1P2 ≦ 0 の場合
- 0 < P1Q1・P1P2 < P1P2・P1P2 の場合
- P1Q1・P1P2 ≧ P1P2・P1P2 の場合
こうして、場合分けは内積の計算のみにより行えるようになりました。
ここまで来れば計算自体は楽です。
- P1Q1・P1P2 ≦ 0 の場合
d = |P1Q1| - 0 < P1Q1・P1P2 < P1P2・P1P2 の場合
d = sqrt(|P1Q1|2 - d22)
(三平方の定理により) - P1Q1・P1P2 ≧ P1P2・P1P2 の場合
d = |P2Q1|
結局 d22 は計算しなきゃならないのですが、距離よりも距離の2乗のほうが計算しやすいし、場合分けにより計算しなくて済むケースもあるので、途中計算では計算を省いたほうがいいでしょう。
二線が交差している場合
この場合、距離は 0 となり、Pn = Qnとなります。
問題はその条件、ですね。
クソ真面目に計算していたらどえらい目に遭ったので、またグーグルさんに助けを求めてみました。
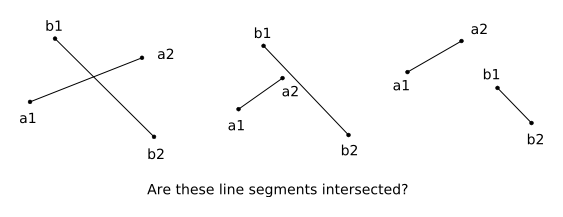
で、見つかったのが以下の記述です。
線分 a = a2 - a1 と線分 b = b2 - b1 が交差している場合,線分 b の端点 b1 と b2 は必ず線分 a の両側にあります。また,線分 a の端点 a1 と a2 は必ず線分 b の両側にあります(上図の左)。逆に交差していない場合,線分 a か線分 b のどちらかから見て,両点ともに片側にある場合が必ずあるといえます。上図の中央の例の場合,線分 a から見れば b1, b2 は線分 a の両側にありますが,線分 b から見れば a1, a2 は両方とも線分 b の右側にあります。これは交差していれば当然のことといえます。
ある点が線分(ベクトル)の左側にあるか右側にあるかというのは,外積を使えば判定できます(下図)。
sinは0度~180度で正の値,180度~360度で負の値を取るので,点がベクトルの左側なら外積は正,右側なら外積は負になります。従って,もし端点が両側にあるなら正と負,片側にあるなら正と正もしくは負と負になるので,2つの外積の値を掛けて正になれば非交差ということが分かります。また,線分 a と線分 b の両方について,相手線分の両端点との外積の値の積が負になれば交差ということが分かります。
(平面幾何におけるベクトル演算 » 直線と線分ページ内 線分の交差判定より)
平面と立体という違いはありますが、要するに交差していない状態じゃなければ交差しているという発想です。
二線分が同一平面上にあるという前提があるので、これとほぼ同じ方法が使えそうです。
さて、二次元から三次元の同一平面上に変化して何が計算上変わるかというと、外積がスカラーからベクトルになります。
この場合、二次元の外積の符号に相当するものは、ベクトルの向きです。
そして、二次元の外積同士の積の符号は、三次元では外積同士の内積の符号に相当します。
そんなわけで、二線が交差する条件は以下のようになります。
二線分が同一平面上にあり、
(P1P2×P1Q1)・(P1P2×P1Q2) < 0
かつ、
(Q1Q2×Q1P1)・(Q1Q2×Q1P2) < 0
で、この条件を満たしたら距離は 0 ってことですね。
二線が交差していない場合
こんなときも

こんなときも
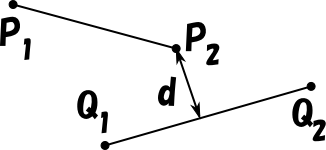
こんなときも
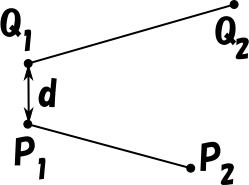
少なくとも一方の線分に属する最近傍点(Pn と Qn の一方または両方)は線分の端点に一致しているわけです。
すなわち、同一平面上にある交差しない二線分の距離は、一方の線分の端点と他方の線分の距離のうち、もっとも短いもの、というわけです。
なので、既にやった点と線分の距離の計算で事足ります。
ちなみに、二線分が平行だったときも同じ方法が使えます。
これで同一平面上にある場合および二次元の場合は完了です。
三次元の場合
二次元から三次元になって何が変わるかというと、ねじれの位置が加わります。
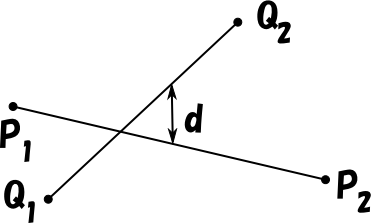
厳密に言えば、同一平面上にない二線分は常にねじれの位置にあるのですが、その中でもねじれの位置特有の計算が必要になるケースがあります。
それは、どちらの線分に属する最近傍点も、線分の端点に一致しない場合です(上図)。
この先は、この特殊なケースを「ねじれの位置」と呼ぶことにします。
距離の計算
さて、この場合はどのような計算をすればいいのかというと、三次元空間上での二直線間の距離を計算すればいいのです。
はい、何気なくさらりと「二直線間の距離」と言いましたね。計算は簡単です。いつものようにネットに答がありましたから。
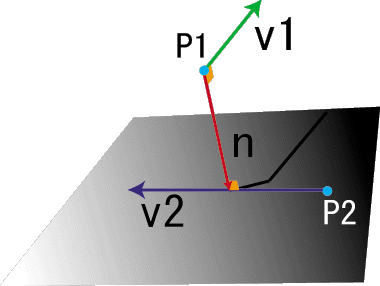
空間に引いた2直線の最短距離を考えて見ます。これは、実は筒同士の衝突判定で必要になります。どうするのか?最短距離とは片方の直線から垂直にもう片方の直線に降りればよいのです。つまり、その降りる線は、2直線の方向ベクトルからなる法線です。
らしく描いてみました。緑と青のベクトルv1,v2がそれぞれの直線の方向を表します。青い点は直線上の一点です。ポイントはv2を含んでいる平面。これは法線ベクトルnとP2があれば定まります。法線ベクトルnはv1とv2の外積から求まりますね。つまり、2直線の最短距離は空間上の点P1から平面までの距離の問題に帰着します。これ、実はこの章内の「ある点から平面までの距離」でもうやっているんですよね。
まとめると、
P1(x1, y1, z1), P2(x2, y2, z2)とし、
ベクトルv12=P2-P1、法線ベクトルn = v1×v2とすると、
求めたい最短距離dは、
d = |n・v12|/|n| と計算できます。法線を標準化すれば、さらに
d = |n・v12| と簡略化できます。
(基礎の基礎編その2 小技集めておきましたページ内 2直線間の最短距離より)
そもそも私が二線分間の距離を問題にしようと思ったのは、今回引用したページのあるマルペケつくろーどっとコムの3D衝突編その6 筒と筒を見て、有限長さの筒について当たり判定を行いたくなったからなんですね。
引用した文章中の記号と、今回計算に使う記号の対応関係は、P1 → P1、P2 → Q1、v1 → P1P2、v2 → Q1Q2、になります。ついでに n はそのまま n として使わせてもらいましょう。
なので、ねじれの位置での二線分間の距離は、以下のように計算できます。
ねじれの位置(ここでは二線分間の距離が二直線間の距離で表せる位置)の場合
d = |n・(Q1-P1)|/|n|
あとは、「二線分間の距離が二直線間の距離で表せる位置」が分かれば完成です。
ねじれの位置の判定
さて、先ほどの計算が成り立つのはねじれの位置の場合だけです。
今回、「ねじれの位置」は、「二線分間の距離が二直線間の距離で表せる位置」としました。
つまり下図のような場合はねじれの位置に含みません。
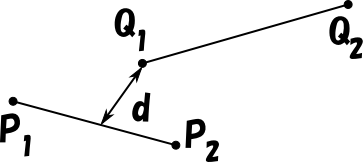
ねじれの位置というのは言ってみれば立体交差のようなものですが、ではどのようにしてその立体交差であるかどうかを判断するのでしょう。
感覚的に言えば、「真上」から立体交差を見下ろせば、その位置から見て交差しているかどうかでねじれの位置かどうかが分かりそうです。

つまり、「上下」方向の成分を無視するということですが、これはどうすればいいのでしょう。
「上下」方向がなくなれば、当然二線分は同一平面上に位置することになります。
逆にいって、「上下」方向に平行移動して、二線分が同一平面上に位置するようにすれば、二線が交差しているかどうかの判定でねじれの位置かどうかが分かるわけです。
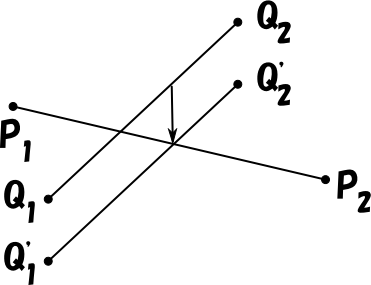
ここで、「上下」方向は、二線分と垂直な方向、移動する距離は、d になります。
二線分と垂直な方向というのはつまり、P1P2 と Q1Q2 の外積方向です。
なので、移動する方向と距離を表すベクトル d は次のようになります。
d = dn/|n|
= (|n・(Q1-P1)|/|n|2)n
と、言いたいところですが、このままだと絶対値記号のせいで n・(Q1-P1) の符号によって移動方向が逆になってしまうので、絶対値符号をはずします。
d = ((n・(Q1-P1))/|n|2)n
んで、この分だけ線分 1 を平行移動すると、二線分は同一平面上に行くわけです。
図と合うように言い換えれば、線分 2 の位置から d を引くと、二線分は同一平面上に来るわけです。
まあ、どっちをどっちに合わせたところで、結果は同じです(数値の精度を考えればちょっとは変わるかもしれんけど)。
今回は図と合わせて、線分 2 を動かすことにしましょう。
移動後の線分 2 の端点を Q'1、Q'2 とすると、
Q'1 = Q1 - d
Q'2 = Q2 - d
となります。
そして、
(P1P2×P1Q'1)・(P1P2×P1Q'2) < 0
かつ、
(Q'1Q'2×Q'1P1)・(Q'1Q'2×Q'1P2) < 0
のときはねじれの位置です。
結果、ねじれの位置のときの距離は次のようになります。
d = |n・(Q1-P1)|/|n|
(n = P1P2×Q1Q2)
ここに来ると Q' が出てこないので注意です。
まとめに代えて
まとめに「代えて」であるからして、まとめていません。
まとめようと思ったら全然まとまらず、同じ事をもう一度書いてしまいました。
こうして見てみると、いくつか計算上のテクニックを使った以外は、基本的な計算を根気よく続けていくことで求められたようです。
基本を根気よく続けながら、単なる基本の組み合わせだけで足りない部分は先人の知恵を借りて突破する、そんな問題解決方法を学んだような気がします。
…終わってから一年以上も経ってからだと何とでも言えますね。
せめて頑張ろうとした痕跡だけでも残しておきます。
分かりやすくまとめてくださる方がいればご連絡ください。
紹介させて頂きます。